Studying patterns

Due to the nature of the genetic optimization, we might obtain different rulebases for the same dataset if we run the experiment with different seeds. Due to the nature of rule-based reasoning, we can directly study how often some patterns appear and how useful variables are by directly analyzing the different rulebases and the way in which their rules use each variable.

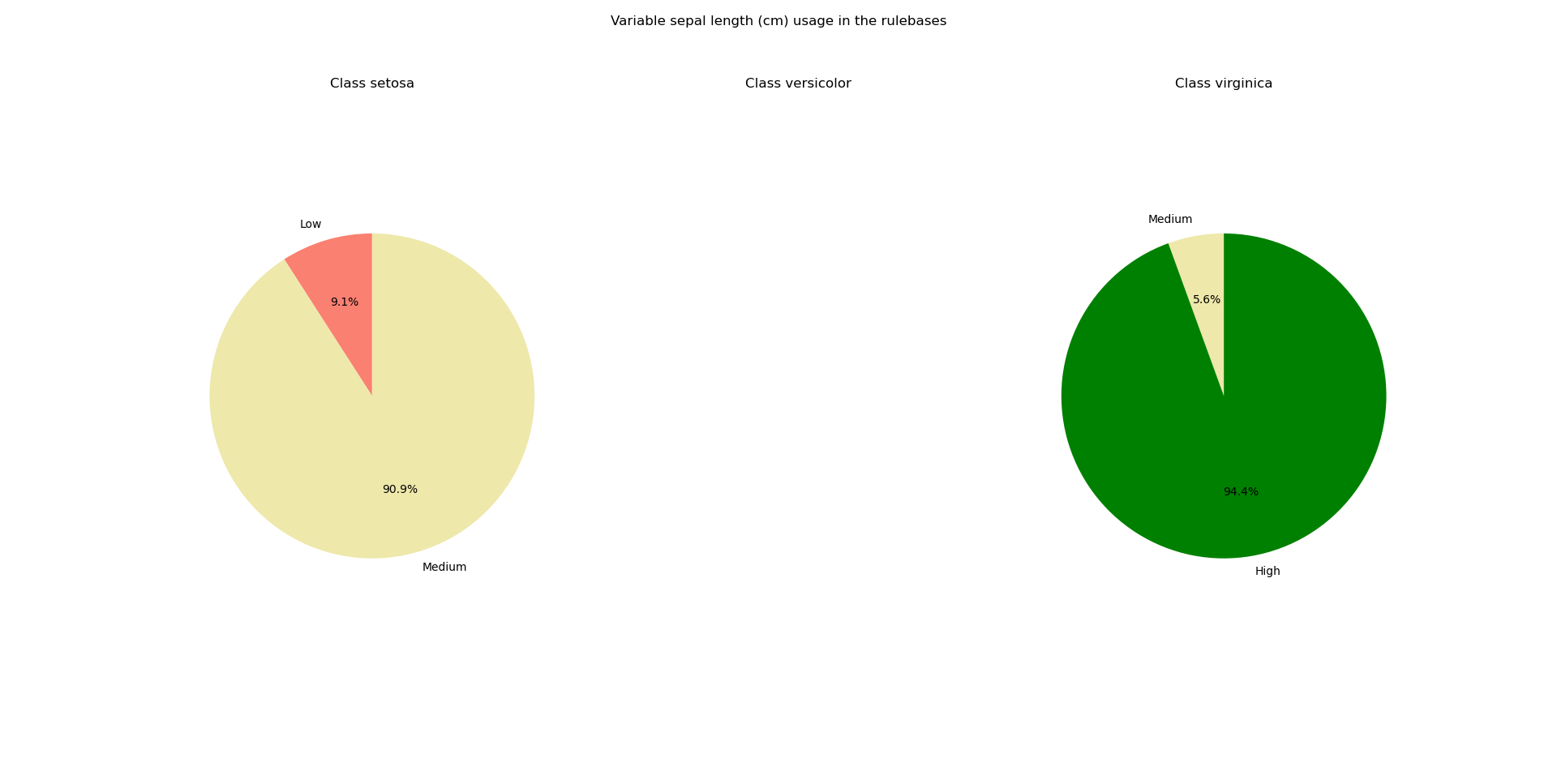
The module ex_fuzzy.pattern_stability contains a series of functions to analyze the ocurrences of the patterns when the same experiment is run with different seeds. This module comes with the class ex_fuzzy.pattern_stability.pattern_stabilizer whose initialization sets the parameters for the analysis. Then, the function ex_fuzzy.pattern_stability.stability_report can be used to run the experiments. Finally, use ex_fuzzy.pattern_stability.pattern_stabilizer.text_report to obtain a text report of the rules obtained and how often they appeared in the experiments. Use ex_fuzzy.pattern_stability.pattern_stabilizer.pie_chart_class and ex_fuzzy.pattern_stability.pattern_stabilizer.pie_chart_var to obtain pie charts of the ocurrences of the variables per class according to the linguistic variables used.

This is an example of a textual report:

Pattern stability report for 20 generated solutions
Average accuracy: 0.89\pm0.07
-------------
Class setosa
Number of unique patterns: 5
Pattern IF sepal width (cm) IS High AND petal width (cm) IS Low appears in 0.80 percent of the trials with a Dominance Score of 0.6426666666666668
Pattern IF sepal length (cm) IS Medium AND petal length (cm) IS Low appears in 0.30 percent of the trials with a Dominance Score of 0.157580748308667
Pattern IF sepal length (cm) IS Medium AND petal length (cm) IS Low AND petal width (cm) IS Low appears in 0.20 percent of the trials with a Dominance Score of 0.11489674513650276
Pattern IF petal width (cm) IS Low appears in 0.15 percent of the trials with a Dominance Score of 0.8502504508114606
Pattern IF sepal length (cm) IS Low AND petal width (cm) IS Low appears in 0.05 percent of the trials with a Dominance Score of 0.7395212506106495

Variable sepal length (cm)
Medium appears 0.50 times
Low appears 0.05 times

Variable sepal width (cm)
High appears 0.80 times

Variable petal length (cm)
Low appears 0.50 times


Class versicolor
Number of unique patterns: 1
Pattern IF petal length (cm) IS Medium appears in 1.00 percent of the trials with a Dominance Score of 0.8733799262279169

Variable petal length (cm)
Medium appears 1.00 times


Class virginica
Number of unique patterns: 5
Pattern IF sepal length (cm) IS High AND petal length (cm) IS High appears in 0.80 percent of the trials with a Dominance Score of 0.7115082780467393
Pattern IF sepal width (cm) IS High AND petal length (cm) IS High appears in 0.15 percent of the trials with a Dominance Score of 0.2558635394456291
Pattern IF sepal width (cm) IS Low appears in 0.05 percent of the trials with a Dominance Score of 0.15428571428571428
Pattern IF sepal length (cm) IS Medium appears in 0.05 percent of the trials with a Dominance Score of 0.04656319290465636
Pattern IF sepal length (cm) IS High appears in 0.05 percent of the trials with a Dominance Score of 0.6360683760683757

Variable sepal length (cm)
High appears 0.85 times
Medium appears 0.05 times

Variable sepal width (cm)
High appears 0.15 times
Low appears 0.05 times

Variable petal length (cm)
High appears 0.95 times

The pie charts look like this: